All models are wrong. Some are useful.
Statistics will never tell you whether the model you have is the true model or not. As a Bayesian all you can do is compare models.
Comparing maximum likelihoods
Consider the straight line model that we adopted last week. In the third class we found a model that seemed satisfactory. Most of the data were consistent with being generated from a straight line model, and a few of the data points were consistent with being outliers: drawn from some other distribution. How do we know that model was any good? We could use a model that is just as "simple" in that it has the same (or fewer!) parameters. Suppose that we could then calculate the log likelihood for our new model, and the log likelihood for our simpler model is higher than the maximum likelihood we ever found for our straight line model. Is the new model preferred? What is that model?
Just because a model has a higher log likelihood doesn't mean that model is necessarily better. A more complex model has more degrees of freedom, and so it may always fit the data better. And a simpler model isn't necessarily better either because it may make very poor predictions elsewhere: it is over-fitting the data.
\( \newcommand\vectheta{\boldsymbol{\theta}} \newcommand\vecdata{\mathbf{y}} \newcommand\vecx{\boldsymbol{x}} \newcommand\model{\boldsymbol{\mathcal{M}}} \)(Re-)Introducing the "evidence"
What we really want is to do is to compare the posteriors of two models. That is we want to compare the model posteriors \(p(\model_1|\vecdata)\) and \(p(\model_2|\vecdata)\). From Bayes' theorem we can describe the model posterior \(p(\model|\vecdata)\) as
\[
p(\model|\vecdata) = p(\vecdata|\model)\frac{p(\model)}{p(\vecdata)} \quad .
\]
Now recall from the definition of conditional probability
\[
p(\phi|\psi) = \int p(\phi|\theta,\psi)p(\theta|\psi) d\theta
\]
we can re-write \(p(\vecdata|\model)\) as
\[
p(\vecdata|\model) = \int_\vectheta p(\vecdata|\vectheta,\model)p(\vectheta|\model) d\vectheta
\]
which you will recall is exactly the (unnormalised) integral we have been trying to approximate using MCMC. The term \(p(\model)\) is our prior belief for the model \(\model\), which may be uninformative. The remaining term \(p(\vecdata)\) is the prior probability of observing the data without reference to any model. That is frightening to think about let alone calculate it, so we will avoid it by computing the odds ratio between two alternative models and force \(p(\vecdata)\) to cancel out
\[
O_{21} \equiv \frac{p(\model_2|\vecdata)}{p(\model_1|\vecdata)} = \frac{p(\vecdata|\model_2)}{p(\vecdata|\model_1)}\frac{p(\model_2)}{p(\model_1)}
\]
\[
O_{21} \equiv \frac{p(\model_2)}{p(\model_1)}\frac{\int_{\vectheta_2}p(\vecdata|\vectheta_2,\model_2)p(\vectheta_2|\model_2)d\vectheta_2}{\int_{\vectheta_1}p(\vecdata|\vectheta_1,\model_1)p(\vectheta_1|\model_1)d\vectheta_1}
\]
Now this is tractable.
If you are still feeling optimistic about Bayesian model selection, that feeling is about to disappear. The integral we need to compute is one over the entire parameter space of each model. That can be extremely computationally intensive, even if the model only has a handful of parameters.
Let's code up an example. First we will generate some data from a polynomial and add Gaussian errors to the observations
\[
y \sim \mathcal{N}\left(\theta_0 + \theta_{1}x + \theta_{2}x^2, \sigma_y\right)
\]
In code, this looks something like:
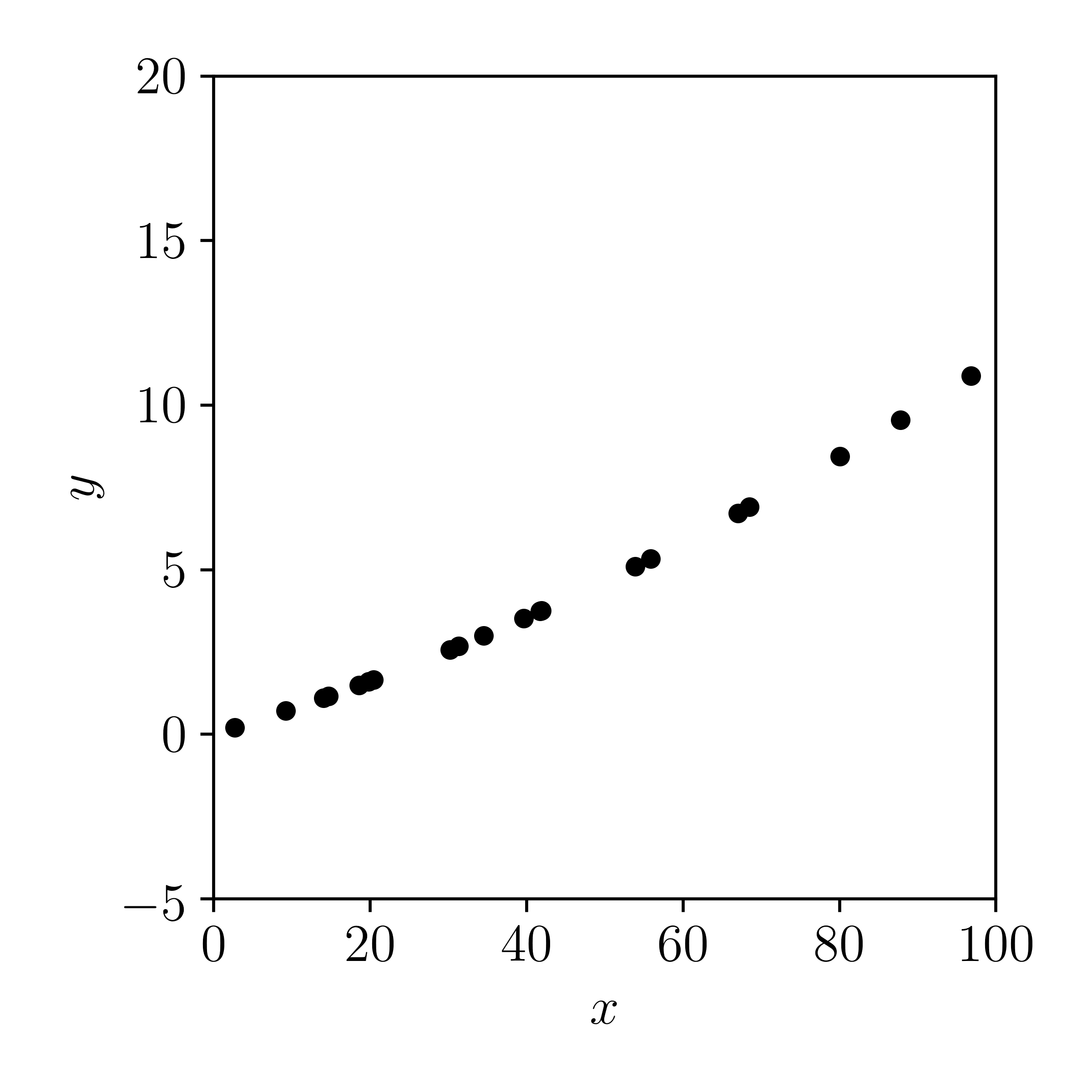
Now let's plot the data with errors added in the \(y\)-direction:
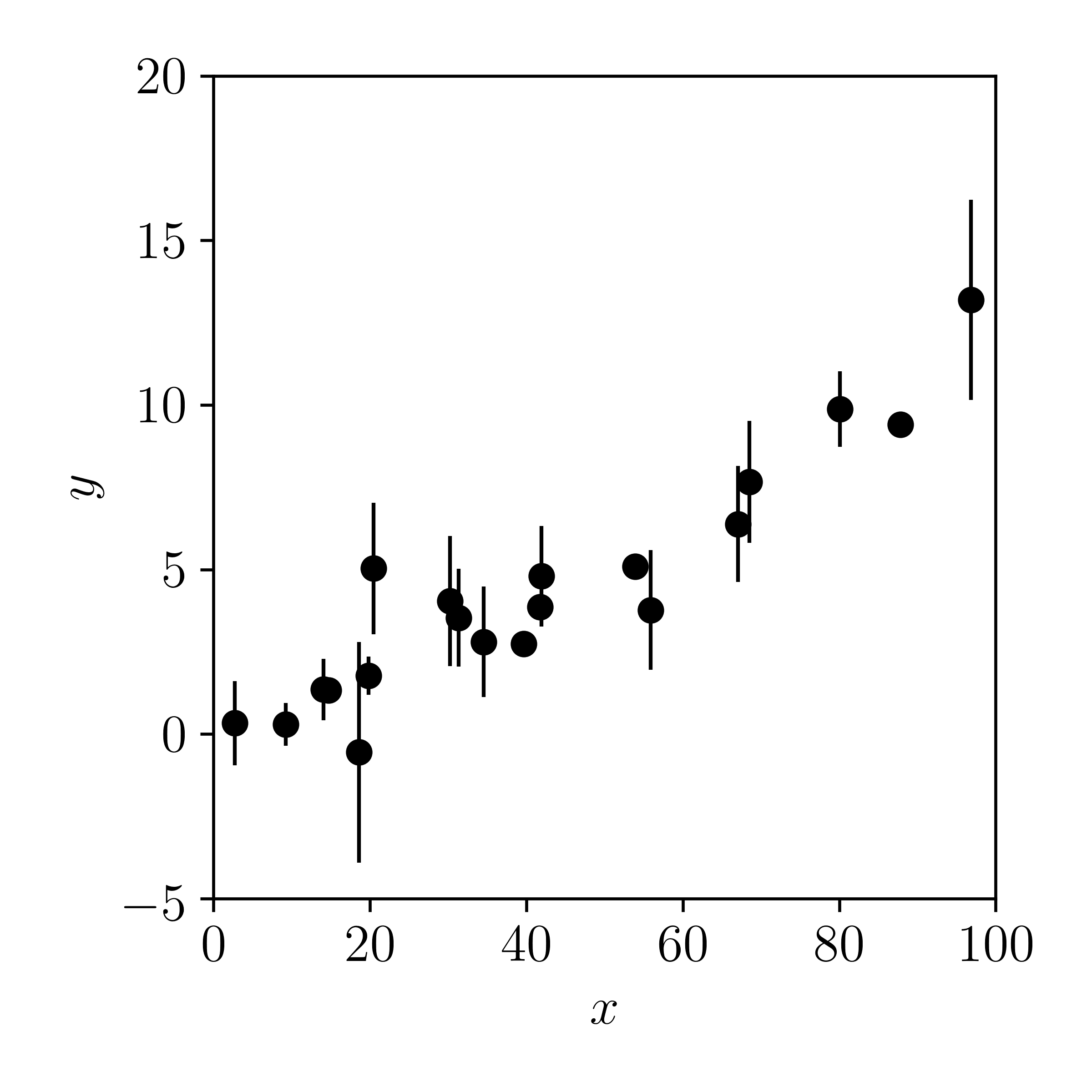
Now imagine if someone gave you this data — without knowing how they were generated — and you were asked:
Are these data better described by a straight line or a polynomial?
Let's calculate the Bayes factor to find out. First we will need to build two models (a straight line model, and a polynomial model), sample the posteriors in each model, and then integrate those posteriors. You could use the Hamiltonian Monte Carlo sampler that you wrote as part of your assignment to sample both models, but normally it is a good idea to build your own sampler to understand how it works (including tuning, diagnostics, etc), and then use a well-engineered implementation for Science™. Here we will use pyMC, a package for doing probablistic programming-esque in Python.pyMC uses the Theano deep learning package to analytically compute gradients, allowing you to use gradient-based MCMC algorithms (and other things) and letting you focus on the model building. Other probabilistic programming languages exist (e.g., Stan and PyStan) and are probably better for specific problems.
Let's build the straight line model first:
Ignore the priors we have put on \(\theta_0\) and \(\theta_1\): they are intentionally set to be extremely broad and to have no impact on our inferences. Let's assume that the chains have converged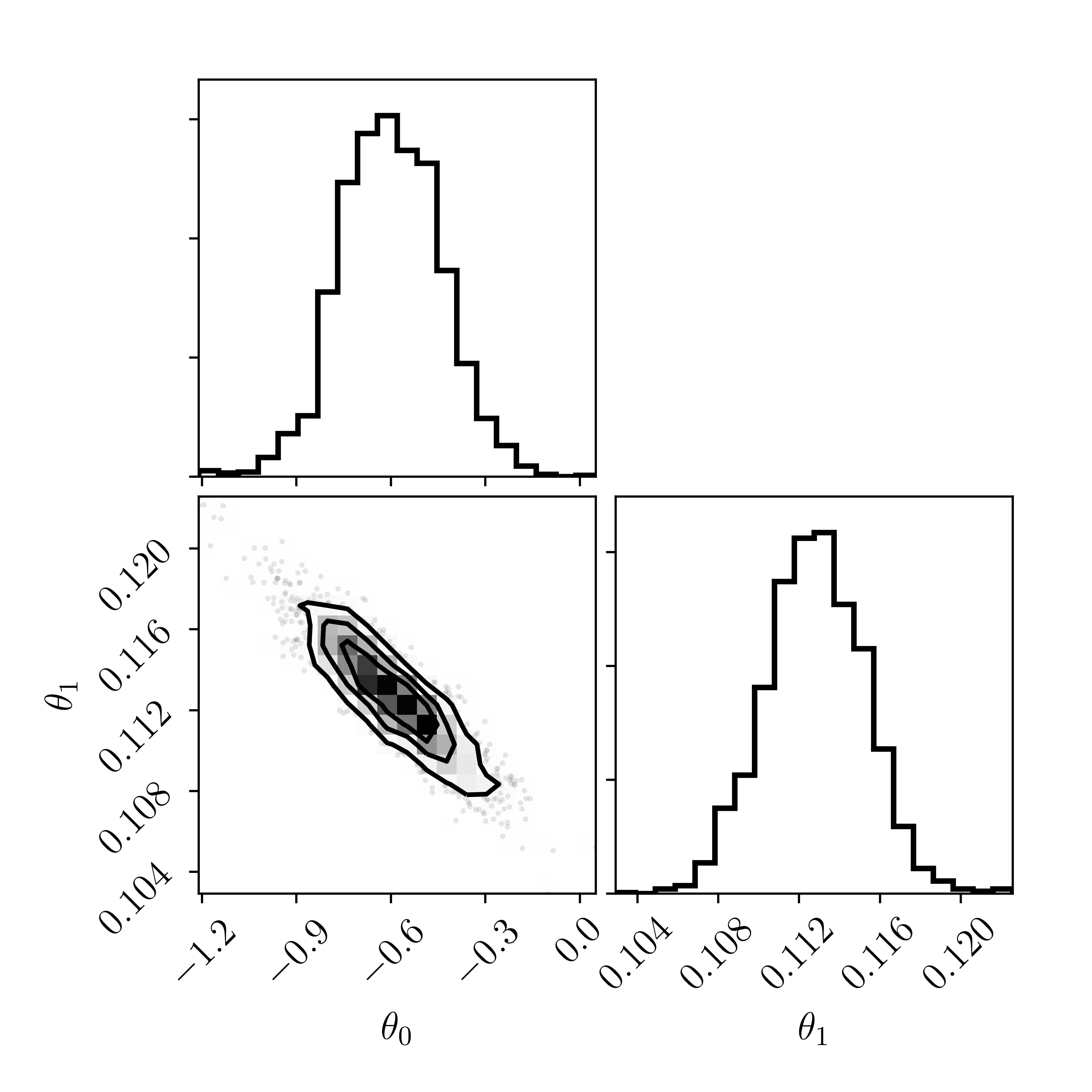
And now let's draw samples from the posterior and make posterior predictions in the data space:
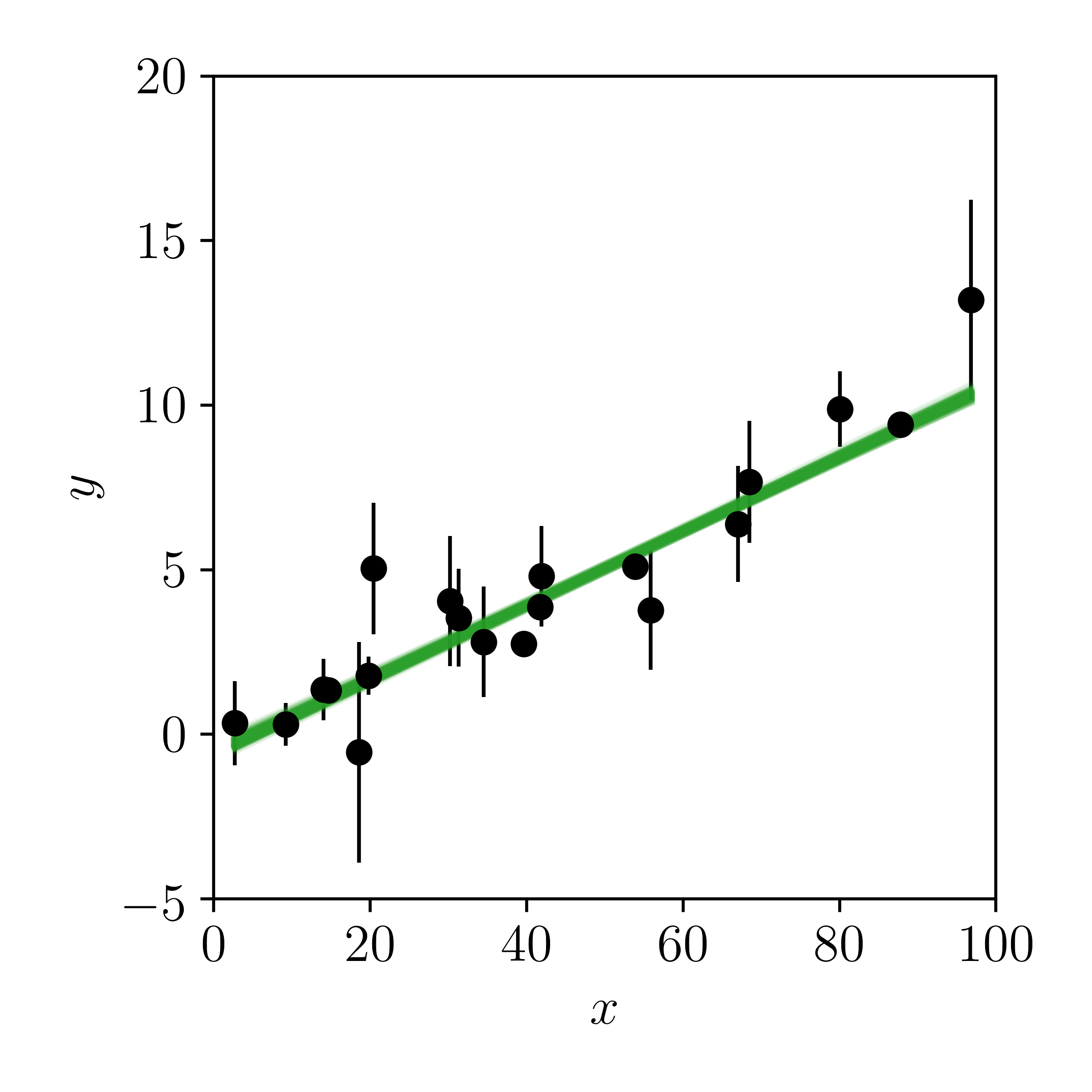
Looks reasonable to me. What do you think? If you didn't know that the data were truely generated by polynomial model, you might conclude from this figure that the data were drawn from a straight line.
Let's build the polynomial model in pyMC:
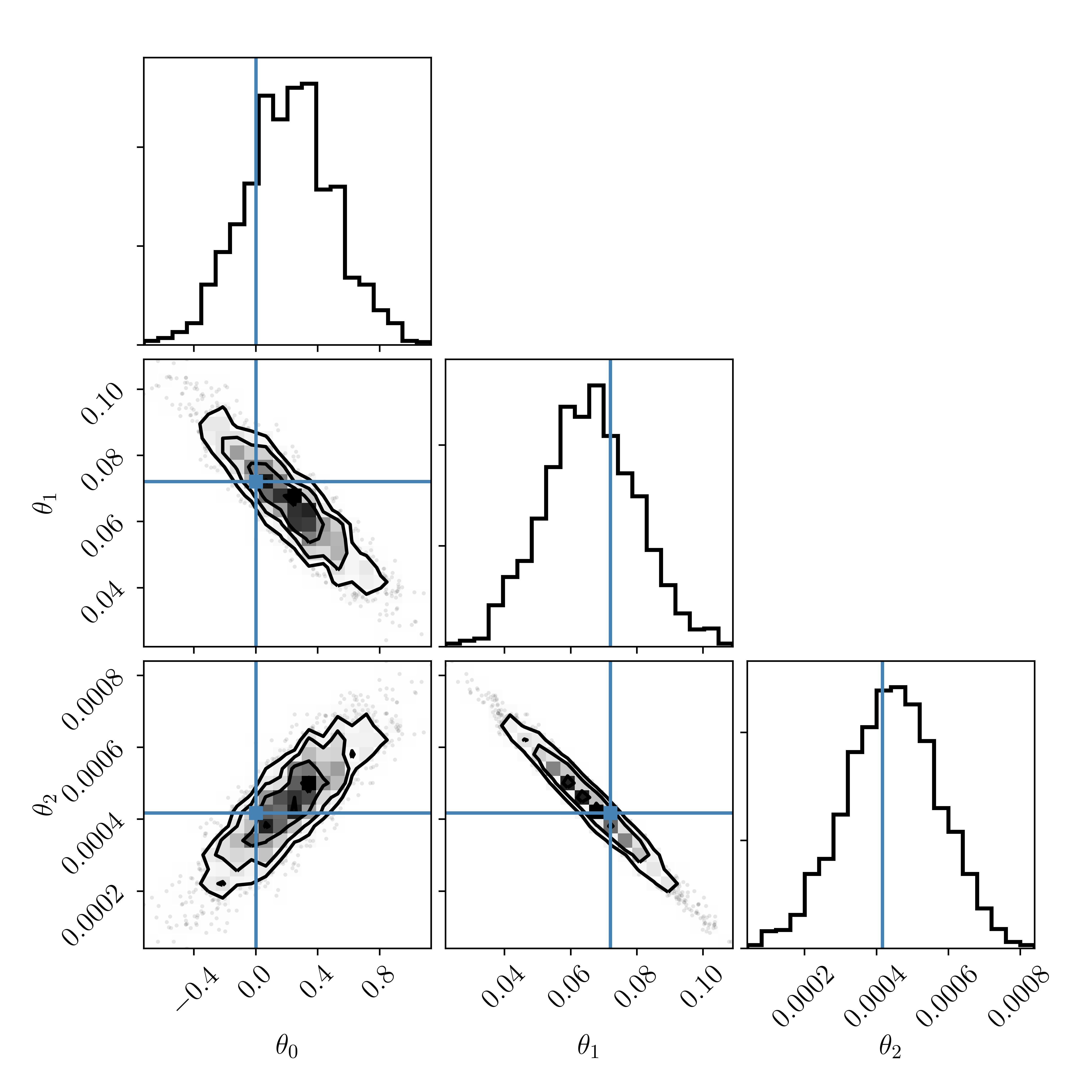
Make a posterior predictive plot, and compare it to that of the straight line model:
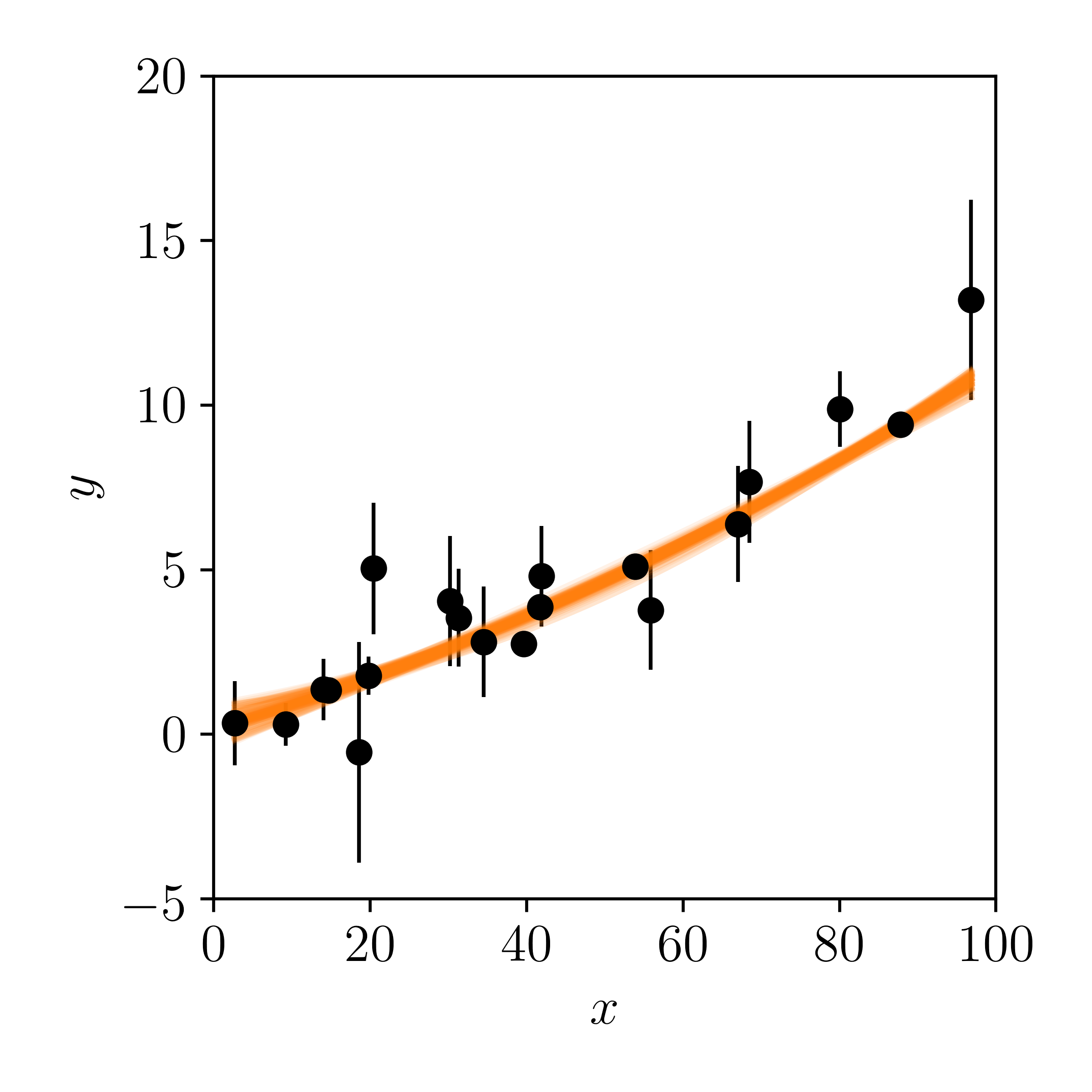
Shrug. They both kind of look good to me. What do you think?
Let's call the straight line model \(\model_1\) and the polynomial model \(\model_2\), and calculate the Bayes factor \(\textrm{BF}_{21}\)
\[
\textrm{BF}_{21} = \frac{p(\vecdata|\model_2)}{p(\vecdata|\model_1)} = \frac{\int_{\vectheta_2}p(\vecdata|\vectheta_2,\model_2)p(\vectheta_2|\model_2)d\vectheta_2}{\int_{\vectheta_1}p(\vecdata|\vectheta_1,\model_1)p(\vectheta_1|\model_1)d\vectheta_1}
\]
which means we must integrate over the posteriors in both model. We will do this numerically. Do the straight line model first. Note that even if we do this numerically, we still have to decide on the limits of the integration. Thankfully we can use the limits of the MCMC draws as the limits of the integration, since we are assuming that the MCMC chains have converged and that the samples drawn are representative of the posterior.
And now do the polynomial model:
From sampling both models and integrating over the posterior samples, you should see output something like this:
Whoa wait a minute! We know that the data were drawn from the polynomial model, and our posterior samples of the polynomial model are pretty much centered on the true values. So clearly our model fitting is working correctly. But the Bayes factor for the true polynomial model is \(\approx\frac{1}{5}\), which implies that the straight line model is favoured by about fives times more than the true polynomial model.
Why is that? Did we do something wrong? When do you think the true polynomial model would be favoured over the straight line model?
<discuss>
Change the MAGIC numbers (as discussed) and re-run the code. How do your conclusions change? How much cheaper or more expensive do your integrals become?
Bayesian Information Criterion
Since the integrals above can be computationally intractable for realistic problems, many have sought to find alternatives. In practice these are all essentially approximations of the evidence for a model, in that the evidence (or normalisation constant) is what you need to compare models, but it's intractable.
The most commonly employed heuristic is that of the Bayesian Information Criterion, \[ \textrm{BIC} = D\log{N} - 2\log\hat{\mathcal{\mathcal{L}}}(\vecdata|\hat{\vectheta}) \] where \(D\) is the number of model parameters, \(N\) is the number of data points, and \(\hat{\mathcal{L}}\) is the maximum log likelihood found for that model. For example, if you had two models \(\model_1\) and \(\model_2\), with \(D_1\) and \(D_2\) model parameters, where each are fit to the same data \(\vecdata\) (which is of size \(N\)), then you will calculate two BIC values \[ \textrm{BIC}_1 = D_1\log{N} - 2\log\hat{\mathcal{\mathcal{L}}_1}(\vecdata|\hat{\vectheta}_1) \] \[ \textrm{BIC}_2 = D_2\log{N} - 2\log\hat{\mathcal{\mathcal{L}}_2}(\vecdata|\hat{\vectheta}_2) \] and you may conclude to prefer the model with the lowest BIC.
Don't be fooled by the name: there is very little Bayes' in this criterion. Under certain conditions it will reduce to something that well-approximates the evidence, but those conditions are rarely met.
The logic of the BIC is that you want a model that fits the data well, with as few parameters as possible. Naively that makes sense: we should restrict the number of parameters because that increases the flexibility and the degrees of freedom. But in practice adding a single parameter tells us very little about how the curvature of the posterior changes. The new parameter could simply be added to the existing model, in which case it makes no substantive change to the log posterior surface. Alternatively it may be introduced as an exoponent on some other model parameter, in which case it will absolutely change the curvature of the posterior. The BIC does not account for those two differences: it only counts numbers of model parameters.
Other information-theoretic approaches do exist, including those that account for such curvature (through the expected Fisher information matrix), but they are outside the scope of this course.
Bayesian decision analysis
Often we are faced with the situation where we don't necessarily need to compare models (over their parameter space), but we need to make decisions. Each decision has some associated utility (e.g., what do we want to achieve) and some associated risk, or risk probabilities for different events. And often the utility of one individual will differ from that of the population, even if their ultimate goals are the same. Let's explore some examples.
There may not be time for this topic. If so it will be done ad-hoc in class with notes (potentially) added later.